Как измерить угол между стенами

Как правильно измерить угол

Какой угол образуют стены. Первый способ — измерение.

Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.

Для чего это нужно делать? — чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.

К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.

Собственно, когда причины выяснили и необходимость измерения угла очевидна — дело за малым — измерить угол.
Если у Вас имеется в домашнем арсенале угломер — тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.

Как измерить угол без специальных инструментов

Первое что необходимо сделать — это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:

• От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм. и ставите точки.
• Далее измеряете диагональ — т.е. расстояние между точками.

Итак например у нас есть три размера — катет 500мм., 500мм. и диагональ 700мм.

Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.

1. Чертим горизонтально отрезок 500мм. с точками «АБ». (см. чертеж ниже.)
2. Чертим окружность с радиусом 500мм. с центром в точке «В».
3. Чертим вторую окружность с радиусом 700мм. с центром в точке «А».
4. В точке пересечения окружностей ставим точку «С».
5. Соединяем точки «В» и «С» отрезком и получаем наш угол.
6. Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.

Когда чертеж построен, мы можем в заключении сделать вывод — измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т.к. 1 градус величина довольно малая.

Какой угол образуют стены. Второй способ — расчёт.

1. От угла отмеряем 1000 мм (чем больше, тем лучше — погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками);
2. Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + b 2 – c 2 ) / (2 • a • b)

Получив cos(γ) угла, далее через функцию arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (1000 2 + 1000 2 – 1500 2 ) / (2 • 1000 • 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.

Как измерить угол?

Смотрите видео

При решении задач в геометрии мы постоянно сталкиваемся с разными фигурами — плоскими и объемными. Большинство геометрических фигур состоит из сторон и углов. Исключение составляют круг, эллипс, шар. Измерение углов — важная часть решения, иногда только правильное измерение и помогает решить задание и найти верный ответ.

Как же правильно измерить угол?

Транспортир — это специальный прибор, в чем то похожий на линейку, который имеет дугу с нанесенной на нее шкалой. Цифры на этой шкале означают градусы. А в градусах, как известно, и измеряют углы.

Как измерить угол транспортиром

Достаточно приложить центр транспортира к точке — вершине угла. Центр транспортира — это маленькая точка под дугой на прямой линии. В нем часто делают небольшое отверстие, чтобы было удобно накладывать его на вершину угла.

Итак, прикладываем центр к вершине, совмещаем прямую линию транспортира с одной из сторон угла — они должны точно совпадать. Затем смотрим, где пересекает транспортир вторая сторона угла. Если она вдруг не дотягивается до транспортира — ее можно немного удлинить пунктиром. В итоге она должна пересечь шкалу на дуге — цифра, которую она пересекает и есть градусная мера угла. Транспортиром можно также рисовать углы, узнайте об этом здесь: Как пользоваться транспортиром

Как измерить угол без транспортира

В некоторых частных случаях угол можно отсчитать по клеткам в тетради. Например, угол 90° рисуется как 2 перпендикулярные линии, выходящие из одной точки. Они совпадают с клетками тетради и по горизонтали, и по вертикали. Если же одна сторона угла совпадает с клетками горизонтально, а другая пересекает каждую клеточку ровно по диагонали, то этот угол будет равен 45°.

Есть также способ измерения угла при помощи часов. Если вы вдруг забыли транспортир, а на руке у вас часы со стрелками, то попробуйте приложить центр часов к вершине угла, одну сторону совместить с цифрой 6, а вторую продлить пунктиром. Одна минута будет равна 6 градусам.

Способ, конечно, не очень удобный, но иногда спасает.

Измерение углов

Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор – транспортир:

У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

Как померить угол между двух стен

Всем привет. Начинается пора ремонтов и в связи с этим обсудим тему геометрии помещения. Всем хочется чтобы стены их жилища были ровные, а комнаты имели правильную прямоугольную форму. Если угол между двух стен не равен 90 °, то мебель, установленная в этот угол, будет постоянно нам об этом напоминать. То же нам грозит если мы будем укладывать плитку или ламинат в помещение с углами не равными 90 °-крайний ряд будет иметь форму клина.

Как померить уже имеющийся угол между двух стен? Есть два способа решения данной задачи.

От угла нужно отложить два одинаковых отрезка АВ и АС длиной 100 см . Они должны лежать в одной плоскости. После этого необходимо измерить расстояние между точками В и С и оно составляет 150 см .

Дальше мы должны начертить отрезок АВ на листе бумаги, но так как он довольно длинный то уменьшим его в 10 раз. Он будет иметь длину 10 см или 100 мм. Из точки А нужно начертить окружность с радиусом 100 мм . Из точки В нужно начертить окружность радиусом 150 мм . Радиус второй окружности в десять раз меньше отрезка ВС .

В точке пересечения двух окружностей ставим точку С . Получили угол ∠ ВАС. Теперь его можно измерить транспортиром и мы получим искомый угол.

Откладываем те же два отрезка от измеряемого угла и измеряем расстояние между двумя точками как и в первом способе. Теперь нужно воспользоваться формулой:

Подставляем наши значения( в миллиметрах) в формулу и получаем:(1000000+1000000-2250000)/(2*1000*1000) = -0,125. Через arccos узнаем сколько это будет в градусах. Искомый угол равен 97.18° .

Если же вы делаете ремонт и хотите выровнять стены, то можно их обшить
гипсокартоном или отштукатурить их. Маяки или каркас нужно выставить таким образом, чтобы будущие стены образовывали угол 90 °. Это можно сделать при помощи лазерного осепостроителя. Начинать нужно со стены с дверью или окном.

Лазерный уровень есть не у каждого хозяина. Тогда можно сделать большой угольник, которым мы будем проверять угол. Угольник можно сделать из ровных планок или профилей для гипсокартона. Нужно взять три отрезка , например 1200 мм, 1600 мм и 2000 мм. Это так называемое правило «три, четыре, пять».

Ведь если мы поделим эти числа на 4 мы получим 3, 4 и 5 частей. Соединив эти отрезки мы получим угольник с углом 90 °.

Онлайн транспортир

Это прозрачный онлайн-транспортир, также помогает измерять углы на изображении, вы можете легко измерить угол любого объекта вокруг вас, сфотографировать и загрузить его, затем перетащить среднюю точку транспортира к вершине угла.

Как пользоваться этим онлайн-транспортиром?

• Вы можете измерить угол любого реального объекта прямо на вашем экране
• Если вы хотите переместить транспортир, перетащите его середину.
• Нажмите на край снаружи транспортира, чтобы добавить к нему метку
• Размещение двух кнопок покажет градусы этого угла
• Двойной щелчок на кнопке удалит ее

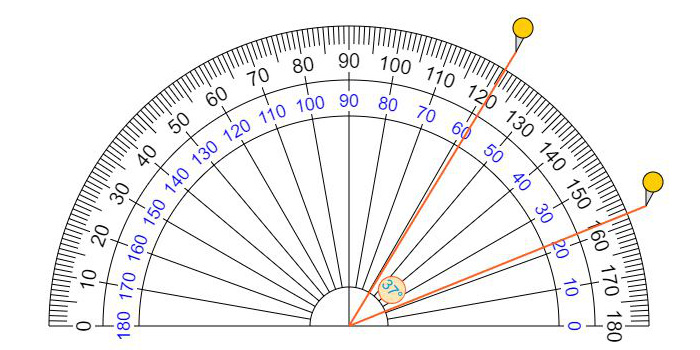
Каждый раз, когда я хочу измерить угол, я всегда не могу найти транспортир. К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.

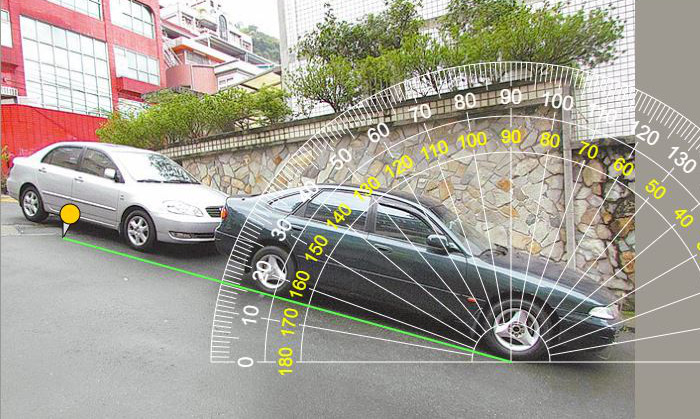
Если вы хотите измерить что-то маленькое, просто поместите его на экран и измерьте прямо; Если вы хотите измерить что-то большее, Вы можете сделать снимок и загрузить его, а затем переместить центральную точку транспортира, чтобы измерить его угол.

Используйте камеру или изображение для измерения угла

Вы можете сфотографировать любой объект, который вы хотели бы измерить, например, автомобиль, дорога, дом, лестница или гора, транспортир прозрачный, после того как вы загрузили изображение, оно будет отображаться в фоновом режиме. затем вы можете убрать транспортир или добавить кнопки, чтобы определить градусы углов, загрузить файл только принять файл изображения в форматах JPG, JPEG, GIF, PNG

На панели управления если цвет фона близок к транспортиру, и это не легко отличить, Вы можете изменить цвет транспортира, чтобы видеть это ясно. Также вы можете переместить его, уменьшить или увеличить размер транспортира, в соответствии с вашими потребностями.

Углы и градусы

• Углы измеряются в градусах. Символом градусов является маленький кружок °
• Полный круг составляет 360 ° (360 градусов)
• Полукруг или прямой угол 180 °
• Четверть круга или прямой угол составляет 90 °

Что вы думаете об этом транспортире?

Посетите эту страницу на вашем смартфоне

Изменить текстовое описание на этой странице

Мы всегда стремимся обеспечить лучший интерфейс и пользовательский опыт, любые предложения по улучшению приветствуются. Текст этой веб-страницы автоматически генерируется Google Translate, это может быть неправильно, если вы хотите предоставить лучшее текстовое описание, пожалуйста, нажмите эту кнопку. ›››
Пожалуйста, будьте вежливы и не используйте это злонамеренно.

Disclaimer:
Use of the protractor within this website is free. Whilst every effort has been made to ensure the accuracy of the protractor published within this website, you choose to use them and rely on any results at your own risk. We will not under any circumstances accept responsibility or liability for any losses that may arise from a decision that you may make as aresult of using this protractor. Similarly, we will not be requesting a share of any profits you may make as a result of using the protractor.

Как высчитать градусы угла

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” />
a” />
b” />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Как вычислять углы

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Количество просмотров этой статьи: 127 859.

В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.

Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны, в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.

Как высчитать угол прямоугольного треугольника в градусах?

Если известны размеры трёх сторон, как высчитать угол в градусах?

Да, треугольник на рисунке не так, чтобы уж очень прямоугольный. Поэтому угол, который можно бы было посчитать за прямой (обозначен на рисунке знаком вопроса), приходится считать по теореме косинусов

1010^2 = 600^2 + 800^2 – 2 cos(a) 600 * 800

cos a = -(1010^2 – 600^2 – 800^2 )/ (2*600*800)=-0,20937

По табличке Брадиса или в своём супер-пупер телефоне находим: 91,2 градуса

Для вычисления углов необходимо обратиться к тригонометрии.

Нам необходимо вычислить величину острого угла А. Для этого используем формулу синуса: ВС/АС (800:1010) = 0,79207920792079.

Зная синус угла А, смотрим в таблицу Брадиса и определяем, что наш угол А равен примерно 52 градусам.

Так как сумма углов треугольника равна 180 градуса, и нам известна величина углов В и А, то мы легко можем узнать величину угла С= 180 – 90-52=38.

Ответ: угол А 52 градуса, угол С 38 градусов.

Математика

Строка навигации

Измерение углов и дуг круга

186. В самом начале курса геометрии было установлено, что значит равные углы, что значит один угол больше другого и что значит найти сумму двух углов, причем, чтобы не делать каких-либо ограничений, надо принять во внимание п. 19, где угол рассматривается, как результат поворота луча около точки (в плоскости). Благодаря этому, углы составляют систему величин, а каждый отдельный угол является определенным ее значением.

Так как здесь налицо те же основные положения, как и при рассмотрении отрезков, то все, что мы нашли для отрезков, справедливо и для углов: также можно измерять углы, принимая один из них за единицу, или находить отношение двух углов.

Чтобы измерять отрезки, нужно было только одно умение (пп. 165 и 172): откладывать на большем отрезке меньший. Так же точно, чтобы выполнять измерение углов, мы должны уметь откладывать меньший угол на большем, – а это мы умеем делать, умеем отличать больший угол от меньшего и умеем строить угол, равный данному.

Что же касается приближенного измерения углов (подобного изложенному в п. 181 для отрезков), то мы можем средствами геометрии лишь выполнять эти измерения с точностью до ½, ¼, 1/8, 1/16 и т. д., так как умеем угол делить только на 2, 4, 8, 16 и т. д. Равных частей. Существуют механические способы деления угла на сколько угодно равных частей.

За единицу при измерении углов принимают прямой угол, в предыдущем курсе мы часто встречались с углами, измеренными прямым углом. Например, если в равнобедренном треугольнике один угол прямой, то каждый из остальных = ½ прямого (½ d), каждый из углов равностороннего треугольника = 2/3 d, сумма внутренних углов n-угольника = 2d (n – 2) и т. д.

Но эта единица оказывается очень велика и на практике берут другую единицу, которая = 1/90 части прямого угла (1/90 d) и которая называется угловым градусом, при письме обозначают эту единицу знаком (°) и, следовательно,

угол равностороннего треугольника = 2/3 d = 60°,
сумма углов треугольника = 2d = 180° и т. д.

Затем вводят еще единицы: угловой градус делят на 60 равных частей, и такую часть называют угловою минутою, – ее знак (‘), угловую минуту делят еще на 60 равных частей и такую часть называют угловой секундою, – ее знак (”).

Например, имеем ¼ d = 22°30′, 1/16 d = 5°37’30”.

Деление прямого угла на 90 равных частей, а углового градуса на 60 равных частей и т. д. Нельзя выполнять геометрически (циркулем и линейкою), а возможно лишь выполнять механическими способами.

187. Упражнения. 1. Часы показывают 25 минут второго. Вычислить в градусах угол между стрелками часов.

2. Вычислить в градусах (минутах и секундах) внутренний угол правильного 8-угольника, 12-угольника, 20-угольника (его еще мы не умеем строить), 14-угольника (его геометрическими способами невозможно построить).

3. Даны 2 угла, найти отношение этих углов, полагая, что при отыскании общей меры этих углов дойдем до остатка, о котором можно, хоть приближенно, принять, что он укладывается в предыдущем целое число раз (наложение одного угла на другой надо выполнять при помощи циркуля).

188. В п. 21 мы научились различать равные дуги одного круга (или равных кругов) и неравные дуги (знаем, что значит одна дуга больше другой), составили понятие о сумме двух дуг.

Надо лишь иметь в виду, что сумма нескольких дуг может оказаться больше всего круга: прикладывая к одной дуге другую, к полученной сумме третью и т. д., можем обойти весь круг и зайти за ту точку, где начинается первая дуга. На основании этих сведений мы также, как и для отрезков, можем утверждать, что дуги одного круга можно выражать числами, принимая за единицу любую дугу. Для выполнения измерения дуг необходимо лишь одно умение, – умение откладывать равные дуги, а это можно выполнять при помощи циркуля, которым можно откладывать равные хорды: равным хордам соответствуют равные дуги (п. 119).

Обычно за единицу при измерении дуг принимают 1/360 часть всей окружности, разделить окружность на 360 частей геометрическими способами мы не можем, можем достигнуть этого механическими приемами (п. 148). Эта единица называется дуговым градусом , дуговой градус делят еще на 60 равных частей и эту часть называют дуговою минутою , разделив последнюю на 60 равных частей, получим дуговую секунду . Знаки для их обозначения употребляются такие же (°, ‘ и ”) как и для угловых градуса, минуты и секунды. Недоразумения здесь быть не может, так как всегда видно, об измерении угла или дуги идет речь. Например,

∠AOB = 56° 8′ 24” и ◡MN = 17° 42′ 5”

(в первом случае угловые единицы, во втором — дуговые).

189. В том случае, когда две дуги одного круга или два угла несоизмеримы, отношение этих дуг или отношение этих углов признается нами равным какому-то иррациональному числу. Однако, мы не можем утверждать, что эти числа таковы же, как и те, которым равны отношения каких-либо двух отрезков: чтобы это утверждать, надо было бы убедиться, что для любой пары углов (или дуг одного круга) можно было бы построить два таких отрезка, чтобы можно было признать отношение двух углов (или дуг круга) равным отношению двух построенных отрезков, т. е. чтобы быть убежденным, что всякое рациональное число, большее одного из этих отношений, больше и другого, и всякое рациональное число, меньшее одного из этих отношений, меньше и другого. Геометрического решения указанного вопроса (построить требуемые два отрезка) вообще не возможно, но общая теория иррациональных чисел позволяет утверждать, что отношение двух несоизмеримых значений одной и той же системы величин (напр., углов) дает иррациональное число, которое можно рассматривать, как отношение двух несоизмеримых отрезков.

190. В частном случае мы можем легко усмотреть, что отношение двух углов равно отношению двух определенных дуг.

Построим круг O (чер. 194) и два центральных угла ∠AOB и ∠COD, которые опираются соответственно на дуги AB и CD. Рассмотрим два отношения ∠AOB/∠COD и ◡AB/◡CD. Найдем самое большое число со знаменателем n, чтобы оно было меньше первого отношения. Для этого разделим ∠COD на n равных частей (выполнить на самом деле такое построение мы можем лишь тогда, когда число n есть степень числа 2, т. е. 4, 8, 16, 32 …, если же число n какое-либо иное число, то все дальнейшее должно основываться на допущении, что существует угол, хотя мы его построить и не умеем, составляющий 1/n часть данного ∠COD) и станем такие углы укладывать на угле AOB, – допустим, что их уложится m с остатком KOB (∠KOB

Как измерить угол между стен. Несколько способов.

Какой угол образуют стены. Первый способ – измерение.

Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.

Для чего это нужно делать? – чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.

К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.

Собственно, когда причины выяснили и необходимость измерения угла очевидна – дело за малым – измерить угол.
Если у Вас имеется в домашнем арсенале угломер – тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.

Первое что необходимо сделать – это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:

• От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм. и ставите точки.
• Далее измеряете диагональ – т.е. расстояние между точками.

Итак например у нас есть три размера – катет 500мм., 500мм. и диагональ 700мм.

Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.

1. Чертим горизонтально отрезок 500мм. с точками “АБ”. (см. чертеж ниже.)
2. Чертим окружность с радиусом 500мм. с центром в точке “В”.
3. Чертим вторую окружность с радиусом 700мм. с центром в точке “А”.
4. В точке пересечения окружностей ставим точку “С”.
5. Соединяем точки “В” и “С” отрезком и получаем наш угол.
6. Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.

Когда чертеж построен, мы можем в заключении сделать вывод – измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т.к. 1 градус величина довольно малая.

Какой угол образуют стены. Второй способ – расчёт.

1. От угла отмеряем 1000 мм (чем больше, тем лучше – погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками),
2. Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + b 2 – c 2 ) / (2 • a • b)

Получив cos(γ) угла, далее через функцию arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (1000 2 + 1000 2 – 1500 2 ) / (2 • 1000 • 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.

Как сделать прямой угол между стенами.

Древнегреческие геометры и, в частности Евклид, старались зря, их знания до советских строителей так и не дошли. В том смысле, что прямоугольных помещений в советских домах не бывает. А бывают в лучшем случае в виде параллелограмма, усеченной трапеции или ромба, а в худшем и наиболее распространенном в виде неправильного четырехугольника.

Это довольно часто затрудняет качественную отделку помещений. Приходится искать прямой угол самому. Сделать это в общем-то несложно.

Разметку проще всего производить на полу. Для этого Вам понадобятся:

• Маркер, мел или карандаш
• Строительный уровень, суровая нитка или строительный шнур.
• Рулетка.

С помощью строительного уровня или отвеса (проще — с помощью уровня, точнее — с помощью отвеса) определите выпирающие участки стен. В этих местах перенесите вертикальные отметки на пол. Проведите через 2 отметки вдоль каждой стены прямые линии так, чтобы остальные отметки (если они у Вас есть) остались между линией и стеной.

Обычно прямая линия вдоль одной из 2 самых широких стен принимается за основу, если нет каких либо других точек отсчета. В этом случае площадь помещения при дальнейшей отделке будет уменьшена минимально.

Отмерьте от одного из углов с помощью рулетки 1 м и поставьте отметку на линии. Сделайте то же самое на перпендикулярной (возможно, не совсем) линии.

Соедините полученные отметки так, чтобы получился треугольник.

Измерьте расстояние между полученными отметками.

Если стены перпендикулярные это расстояние должно равняться ~ 1.414 м более точно 1.41421356 м, но такая точность вам не понадобится.

Если расстояние (гипотенуза треугольника) больше, то у Вас вместо прямого угла между стенами тупой. Для того, чтобы получить прямой угол, приложите начало рулетки к точке пересечения линий в углу и нарисуйте небольшую дугу радиусом 1 м. Затем приложите начало рулетки к отметке на линии вдоль стены принятой за основу и нарисуйте небольшую дугу радиусом 1.414 м. Проведите через точку пересечения дуг и точку пересечения линий в углу прямую линию.

Эта новая линия и будет контуром стены. Если это для Вас слишком сложно, то просто отмерьте на гипотенузе 1.414 м от отметки у той стены которую вы приняли за основу. Проведите прямую линию через полученную отметку и точку пересечения линий в углу. В этом случае Вы получите не прямой угол, но все же намного ближе к прямому, чем тот который был.

Если расстояние (гипотенуза треугольника) меньше, то у Вас вместо прямого угла между стенами острый. Для того, чтобы получить прямой угол, отступите от отметки на линии вдоль стены, принятой за основу, несколько сантиметров. Нарисуйте на полу небольшие дуги по принципу, изложенному в предыдущем пункте. Полученную линию можно перенести ближе к стене. Главное условие — отметки выпирающих участков стены должны остаться между новой линией и стеной.

Если Вы не совсем поняли этот текст, то рисунок поможет Вам лучше разобраться:

От полученных 2 сторон прямоугольника методом параллельного переноса определяются оставшиеся 2 стороны.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)).

Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Конечно можно и так, через корень из двух.Но я обычно использую метод 3-4-5(египетский треугольник). Берем любую длину за единицу.Откладываем ее содной стороны 3 раза, с другой 4 . Гипотенуза соответственно должна получиться 5 выбранных единиц.И никаких дробей,все целочисленно.Ну а перенос тот же.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Как найти прямой угол какие есть углы Математика

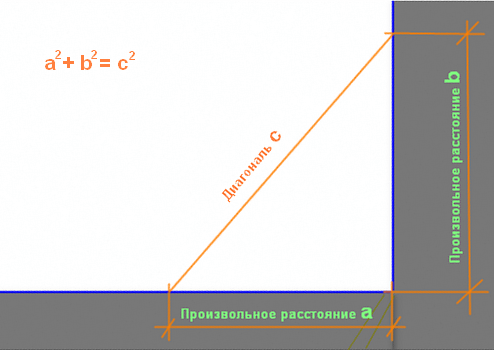
1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.

Илл.1. Построение Золотого, или египетского треугольника

• Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
• Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
• Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
• В момент натяжения на линии границы – точка А, вбиваем колышек.
• Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
• После этого натягиваем мерку R5 – от А до В.
• В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.

2й способ. С помощью циркуля.

Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент

Наш циркуль-шагомер имеет шаг в 1 метр.

Илл.2. Циркуль-шагомер

Построение – также по Илл.1.

• От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
• Ставим ногу циркуля в точку О.
• Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
• Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
• Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
• Проводим прямую (отрезок) через точки С и D.
• Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
• На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
• Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.

Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля

Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.

• Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.

Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки

• Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..

Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.

Листочек в клеточку

На листике в клеточку легко можно сделать замеры тех же стандартных углов, что и в предыдущем варианте.

1. Определить 90 градусов будет легче всего – нужно просто нарисовать квадрат.
2. Проведя в квадрате диагональ можно получить угол 45 градусов.
3. Чтобы определить 30, 60 градусов нужно нарисовать прямоугольник (5 клеток в длину, 3 в высоту). Проведя в нем диагональ, получим угол 30 и 60 градусов. Если разделить линией угол 30 на 2 части, получим 15 градусов.

Полученные углы нужно вырезать и сравнить с заданным углом. Обычно, после прикладывания заготовок, получается, визуально определить примерные показатели.

Видео

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

1. Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
2. Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
3. В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
4. После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
5. Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
6. Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
7. В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
8. Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Способы определения разворота

Раньше распространенным решением как вывести угол 90 градусов, например, на фундаменте был обычный строительный уголок. Главное, чтобы он был проверен и соответствовал 90 градусам. Сегодня профессионалы для упрощения процесса и ускорения монтажных работ пользуются лазерными уровнями. Третий вариант – применение обычной измерительной рулетки.

Обычная строительная рулетка

Теорема Пифагора

С этой доказанной теоремой знаком каждый, кто учился в школе. Она применима только к треугольникам, в котором один из углов обязательно прямой. Прилегающие к нему стороны – катеты a и b, соединительный отрезок – гипотенуза (с). Формула выглядит так: a²+b²=c².

Удобство использования такого способа как найти прямой угол при строительстве в том, что наносить разметку можно в любом по площади помещении. Здесь даже допустимо наличие посторонних предметов. Главное, чтобы был доступ к углу и стенам, можно было свободно протянуть соединительную гипотенузу. Дополнительно понадобится только калькулятор, чтобы быстро произвести нужные вычисления.

Египетский треугольник

Золотой или Египетский треугольник – это фигура с прямым углом, у которой стороны равны 3, 4 и 5 частям. Удобство здесь заключается в том, что не нужно возводить параметры в квадратную степень и извлекать корни. Достаточно принять за часть ту или иную условную единицу. Это может быть как 1 см, так и 10 метров, что особенно удобно для решения как вывести угол 90 градусов на стенах из штукатурки.

Если имеются сомнения в справедливости утверждения про угол в 90 градусов, то можно его проверить с помощью теоремы Пифагора: 3*3+4*4= 5*5 или 9+16=25. Остается только начать применять эту методику на практике.

Равнобедренный треугольник

Здесь рассматривается для удобства формирования угла 90 градусов с помощью рулетки фигура с двумя сторонами, которые равны 100 см. Если между ними прямой разворот, то длина основы составит 141,4 см. Актуален такой подход в строительстве потому, что при увеличении метровых ориентиров в 2, 3 и более раз разница между размерами соединительного отрезка будет идентичной. То есть в прямоугольном равнобедренном треугольнике справедливы такие равенства:

• a и b равны 100*2=200 см – c=141,4*2=282,8 см;
• a и b равны 100*5=500 см – с= 141,4*5=707 см;
• a и b равны 100*2,2= 220 см – с=141,4*2,2=311,08 см.

Если проверить эти утверждения, то гипотенуза или основа равнобедренного треугольника с верхним прямым углом будет при округлении действительно равна 141,4 (141,421356…). С одной стороны – это простой и верный способ как проверить угол 90 градусов рулеткой по нанесенной разметке. Достаточно отмерять метровые участки и сделать только одно умножение 141,4 на число метров. Один только недостаток здесь все же есть. Если в квартире или доме погрешность будет несущественной из-за малых габаритов, то на крупных объектах отклонение из-за неточной гипотенузы может стать заметным.

Коротко главном

В интерьере часто приходится выводить прямые углы под мебель или сантехническое оборудование.

С помощью рулетки можно проверить разворот в 90 градусов тремя способами: стороны равны 3/4/5 частей, если между метровыми стенками соединительный отрезок составляет 141,4 см, применяя теорему Пифагора.

Также рулетки достаточно для формирования трех углов в 30, 45 и 60 градусов.

Дополнительно может понадобиться только калькулятор и карандаш для нанесения разметки.

Где нужен угол 90 градусов между стенами. Как вывести угол 90 градусов между стенами своими руками

Качественный ремонт и отделка подразумевает хорошую геометрию помещения. Без выверенной геометрии, хотя бы в самых нужных местах, хороший ремонт сделать не удастся. Здесь я расскажу как сделать угол 90 градусов между стенами своими руками и о том, где он действительно необходим.

Где нужен угол 90 градусов между стенами

Углы под 90 градусов в основном везде по квартире не выводятся. В эконом-ремонтах, да и в большинстве евро-ремонтах, выведенные в 90 градусов углы необходимы лишь в двух местах:

1. в том углу, где будет висеть/стоять кухонная мебель,
2. и в ванной комнате, где будет стоять сама ванна, в двух смежных углах (или в одном, если душевая кабина стоит в углу). Или по всем 4-м углам ванной, поскольку там будут стоять раковина, стиральная машина и т.п.

В остальных случаях — всё на желание заказчика или человека, осуществляющего ремонт своими силами.

Чем проверять и выставлять углы

Угол легко проверить строительным угольником, можно приобрести в магазине, если собираетесь выводить углы, он будет вам необходим.

Строительный угольник необходим для проверки углов

Просто прислоняем угольник к внутреннему углу. Наружные углы мы пока рассматривать не будем, ради понимания самого процесса. После понимания как выравнивать внутренние углы под 90 градусов своими руками, внешние для вас проблем не составят.

Проверяем внутренний угол

Смотрим, что получается. Если всё нормально, зазоров между угольником нет, то расслабьтесь. Если зазор превышает 5 мм, то следует насторожиться и узнать как выровнять такой угол в прямой, что бы и ванна и шкафы висели хорошо. Дело в том, что зазор в 5 мм под небольшим, пускай полуметровым (в длину хотя бы одной грани) угольником, на всю длину стены оказывается довольно крупным и в конце стены может достичь и 5 см.

Делаем угольник самостоятельно

Угольник можно соорудить и самостоятельно, причём любого размера. Удобнее всего делать такой угольник из гипсокартонных профилей 27*28 мм (жёстких или полужёстких).

Пользуемся пра́вилом египетского треугольника, при котором: если катеты угла равны 3 и 4 частям, а гипотенуза 5 частям, то угол будет прямоугольным (прямой угол между катетами).

Надрезаем и сгибаем нужной длины профиль посредине (стороны нашего угольника не обязательно должны быть равны 3 и 4 определённым нами частям, пра́вило нужно лишь для того, чтобы сделать прямой угол). Сгибаем, принимаем за 1 часть, к примеру, 30 см. Чем больше вы сделаете часть, тем «прямее» получится угол.

Отмеряем на одном катете 3 части — 90 см, на втором 4 части — 120 см. Делаем отметки маркером. Далее, сгибая угол, отмеряем строго от отметок гипотенузу — 5 частей — 150 см. Наш угол прямой, осталось его зафиксировать тем же профилем на саморезы. Тут следует быть аккуратным, чтобы не сбить угол, проверьте правильность разметки несколько раз.

Ниже в ролике наглядно показано как соорудить такой угольник

Проверяем угол с помощью лазерного построителя плоскостей

Лазерные построители плоскостей позволяют с лёгкостью выверять вертикали, горизонтали, отклонения целых площадей, а так же и углы, если такая функция на нём предусмотрена.

Лазерный построитель плоскостей, с функцией построения прямого угла

Не все построители плоскостей подходят, а те которые проецируют две перпендикулярных вертикальных плоскости. С ним работа гораздо облегчается, но стоит такой прибор начиная от 15 тыс. руб. Можно найти и подешевле, особенно в Китае, но у них могут быть и отклонения, хоть часто и не значительные, они как минимум, написаны в паспорте устройства, а на дешёвых моделях отклонения могут и вовсе не совпадать с паспортными. Проверьте это перед использованием с помощью большого угольника, который описан выше или на заведомо прямых углах.

Такие приборы позволяют не только выводить прямые углы, а так же и → штукатурные плоскости и → стяжку пола (по ссылкам рассказано как делать штукатурку по маякам и цементно-песчаную стяжку).

Лазерный построитель плоскостей (нивелир) стоит лишь включить, приставить к углу и прочертить линии на полу, которые он спроецировал. Далее я расскажу как проверить углы и выстроить прямоугольник на площади помещения с помощью угольника и правила, а как работать лазерным построителем плоскостей станет понятно из этого рассказа.

Делаем разметку под выравнивание прямых углов

Возьмём для примера ванную комнату и предварительно проверим углы угольником по всей площади и посмотрим примерно какая картинка у нас вырисовывается.

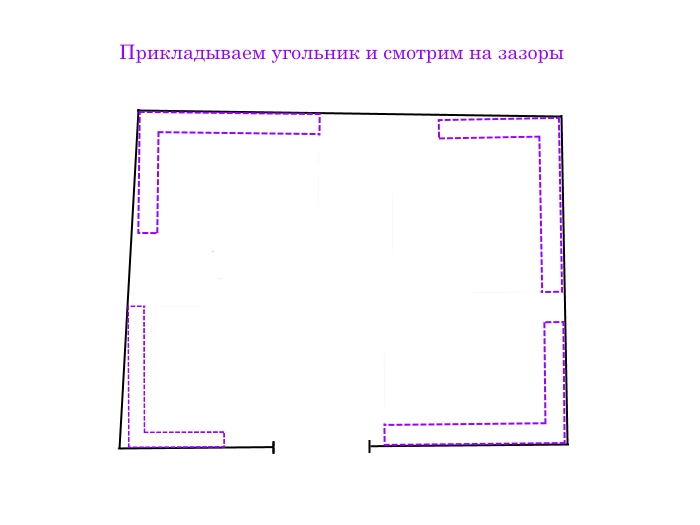
Угольником проверяем углы

Картинка у нас совсем не радостная, один угол (левый нижний) совсем ушёл. С остальными углами всё более-менее, но ванная напротив двери не встанет, точнее встанет, но образуются зазоры между ванной и стеной. Небольшие зазоры можно перекрыть плинтусом для ванн (3-5 мм, даже до 1 см), а вот больше уже ничем не перекроешь. Точнее, и больше можно, хоть 3-5 см, но качество… качество будет совсем не то.

Давайте теперь сделаем тоже самое, только удлиним наш угольник прави́лом и от угла к углу в итоге начертим внутри нашего помещения прямоугольник.

Начинаем разметку от первой стены

Первым делом проверим нашу первую стену на вертикаль и плоскость. Если выравниваем 2 угла, то это стена, параллельная ванне, если выравниваем 4 угла (всю площадь), то стена с проёмом. Если стена завалена, её нужно будет выровнять первым делом, но не торопитесь, ведь мы ещё не проверили всю площадь.

Для начала просто отобьём ровную линию параллельно первой стене, максимально приближённую к ней.

Проведём первую линию, параллельно первой стены

Далее между первой стеной и второй стеной установим угольник одной гранью параллельно первой линии, а на вторую грань угольника накладываем прави́ло. Совмещаем грань прави́ла и угольника, тем самым «удлинняя» наш угольник. Чертим линию на полу до конца стены максимально приближённую к стене. Регулируем и совмещаем наш увеличенный угольник так что бы:

• линия была ровной,
• расстояние до стены минимальным,
• вторая грань угольника была параллельна первой линии.

Так получаем первый прямой угол.

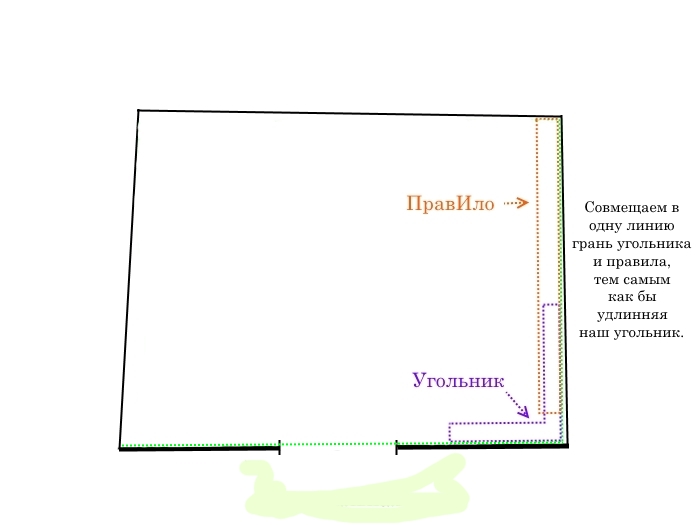
От первой линии отобьём вторую, перпендикулярную ей

Далее идём на следующий угол, до которого мы чертили линию, и совмещаем угольник одной гранью параллельно второй линии. Повторяем процедуру с правилом (совмещаем его с угольником) и чертим третью линию перпендикулярную второй, опять же максимально приближённую к стене.

Тут требуется некоторая сноровка, чтобы совмещать прави́ло, угольник и делать прямой угол с линиями, максимально приближёнными к стене (это делается для того, что бы при штукатурке «не съесть» лишнее пространство). Если прави́ла не хватает, дочерчиваем до куда хватает, переставляем прави́ло, совмещая его с линией, и проводим её до конца стены.

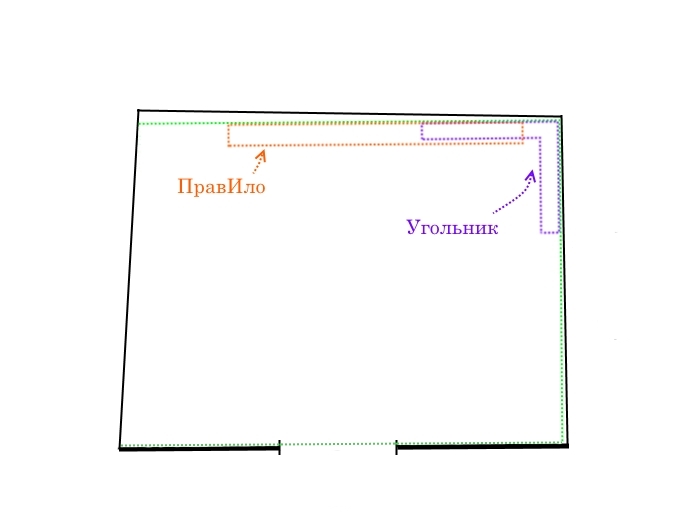
Чертим третью линию перпендикулярную второй

Чертим четвёртую линию, по аналогии. В итоге у нас должен получится начерченный на полу прямоугольник внутри нашего помещения. Проверяем его по первой грани — по стене с проёмом, так же, прикладывая угольник и правило.

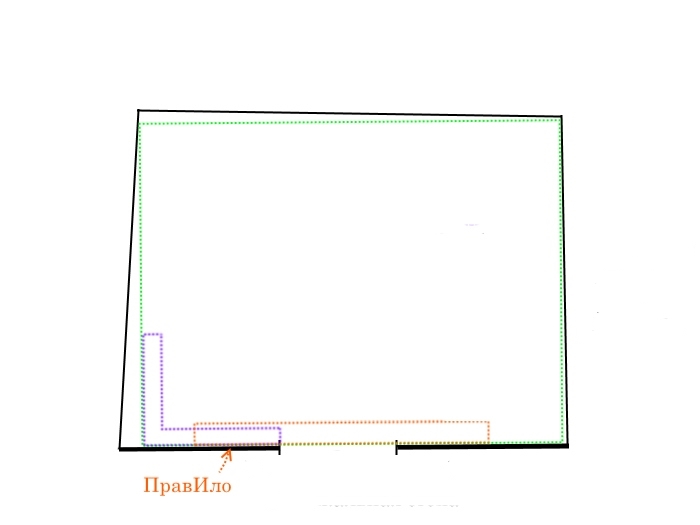
Проверяем по 1-й грани полученный прямоугольник

Если всё ровно, можно немного расслабиться. Если нет, повторяем процедуру и/или смотрим где ошиблись.

Как вывести углы в ванной: все углы 90 градусов или только два

Теперь, когда мы знаем что нам грозит, можно попробовать сделать разметку под 2 угла и посмотреть, что нам грозит в этом случае. Делаем всё тоже самое, только за основную, первую стену берём противоположную проёму (стену, параллельную ванне).

1. Прочерчиваем линию параллельно первой стены.
2. Выставляем угольник и прави́ло по двум углам.
3. Прочерчиваем линии к стене с проёмом.

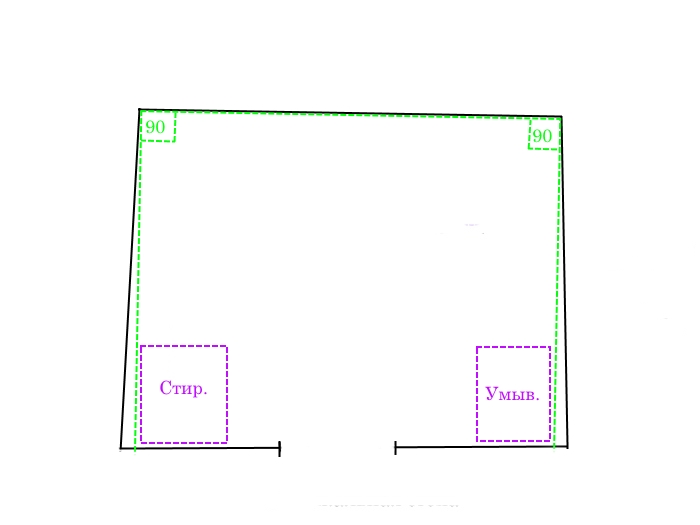
Смотрим, что получится, если выровнять 2 угла

Вот что получилось. Стену с проёмом и стену напротив мы выводим только в вертикаль и 2 угла по 90 градусов, там где ванна. Расход штукатурки и трудозатрат меньше. Углы примыкающие к стене с проёмом получаются не такие страшные. Зазор если и есть, то он небольшой.

Определяемся с углами

Определимся будем выводить прямые углы только там, где ванна или во всех углах. Обращаем внимание на другую сторону стены, которая в коридоре. Если стена с проёмом завалена, то со второй стороны стены нужно будет так же выполнить штукатурку и вывести её в вертикаль, иначе не получится ровно установится дверь.

Важный момент, если начинать от стены с ванной, то углы со стеной с проёмом вывести уже не получится, т.к. начиная от стены с ванной, все неровности «выползут» на стену с проёмом и может оказаться так, что с одного края проёма толщина стены будет 10 см, а с другой все 15 см. И как в такой проём устанавливать дверь, совершенно не понятно…

Выравнивать стены нужно начинать от стены с проёмом, если выравниваете все углы, а если только два угла, то первой выравнивается стена параллельная ванне.

Проверяем вертикальность стен

Теперь, когда мы выстроили наш прямоугольник, проверяем стены. Тут дело в том, что полученный квадрат может не получиться из-за кривизны стен и придётся сдвигать его грани от стены. Проверяем прави́лом с пузырьковым уровнем или правилом с прислонённым к нему пузырьковым уровнем или отвесом, что не совсем удобно. Посмотрим как проверить стену правилом и пузырьковым уровнем.

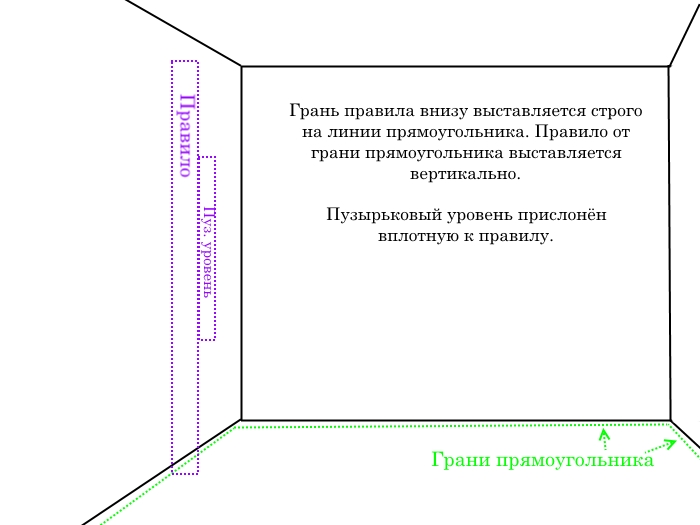
От граней прямоугольника смотрим возможность вертикально выровнять стены

Прави́ло нижним краем выставляется на грань прямоугольника. Прави́ло выставляется вертикально, пузырьковый уровень вплотную прилегает к прави́лу. Важно, что бы прави́ло и уровень были чистые, не было наслоений сухой штукатурки — это априори.

Проходим по стенам, особенно по углам и смотрим возможность их выравнивания. Если где-то выставить прави́ло вертикально от грани прямоугольника не получается, потому-что мешает стена, грань прямоугольника необходимо сдвинуть на то расстояние, которое требуется для выравнивания стены и установки маяков.

Следует помнить, что маяки имеют толщину 6 мм. Просматривайте стены исходя из того, что на ней нужно будет размещать маяки.

Грань сдвигается от стены параллельно противоположной грани на одинаковое расстояние с обоих концов.

Установка маяков и штукатурка стен

Дальше всё просто (относительно) и сводится к → установке маяков и → штукатурке стен по маякам, с одним условием, что при установке маяков проверяется ещё и угол 90 градусов.

Нижняя грань маяка размещается на линии прямоугольника и маяки выставляются вертикально по прави́лу. При установке маяков следует проверить углы с помощью правила и угольника. Единственное, что первой выводится стена, от которой мы «плясали», то есть для четырёх углов — стена с проёмом, для двух — стена с ванной. Сначала следует вывести её в вертикаль, об ращая внимание на то, сдвинулась ли при этом грань прямоугольника от стены, что в целом не страшно, но нужно понимать, что ваша ванная станет такого размера, как прямоугольник и поместится там всё что вы задумали или нет, нужно предусмотреть заранее. Так же нужно учитывать что помещение уменьшится на толщину плитки и раствора (если плитки) как минимум на 0,8 см с каждой стороны стены.

На этом эту статью можно завершить, поскольку дальнейшие работы сводятся, как уже сказал к установке маяков и штукатурке по маякам. Так же, если у вас ванная комната с внешним углом, то вы без труда сможете его вымерить и вывести, использую пример, описанный выше. Если вы выравниваете угол на кухне, то всё происходит так же, выравнивается просто один угол. Если у вас помещение побольше, не ванная комната, то чертить прямоугольник лучше под лазерный построитель плоскостей, но под правило тоже можно (2-2,5 метра). Успехов!