Как научиться правильно клеить обои

Как правильно клеить обои

Настенные обои — это лицо вашей кваритиры. Правильный выбор и оклейка обоев способны не только подчеркнуть индивидульный стиль комнаты, но и создать нужную атмосферу. В данной статье приведена примеры и нюансы, необходимые для идеальной оклейки и долгого срока службы обоев

Шаг 1 : Подготовка поверхности

Для оптимального наклеивания поверхность должна быть сухой, чистой и обезжиренной. Старые, плохо приклеенные обои и отстающие слои краски необходимо удалить. Трещины и дыры заделать шпаклёвкой. Поверхности с повышенной гигроскопичностью и осыпающиеся поверхности предварительно обработать грунтовкой глубокого проникновения, облегчающей смену обоев.

Шаг 2 : Приготовление клейстера

Универсальный клейстер высыпать, энергично размешивая, в холодную воду и некоторое время продолжать размешивать. Через 30 минут ещё раз размешать. Клейстер готов к применению.

Шаг 3 : Нанесение клейстера и наклейка обоев на поверхность

При нанесении клейстера на обои:

Флизелиновые обои с совмещением рисунка.

Обои равномерно намазать клейстером, сложить и дать им размягчиться. Через некоторое время наклеить обои встык и прокатать валиком.

При нанесении клейстера на поверхность (только при использовании текстильных обоев):
Нарезанные полотна обоев примерно за 5 минут до наклеивания слегка смочить с обратной стороны, чтобы избежать образования пузырьков воздуха. Клейстер равномерно нанести по ширине 1 — 2 полос обоев при помощи валика. Затем положить обои на слой клея и прижать. Спустя короткое время, обработать стыки гладким роликом для швов.

Также необходимо обращать внимание на рекомендации изготовителя обоев!

Когда обои уже наклеены, лучше всего хотя бы на сутки закрыть комнату, чтобы в ней не было сквозняка. Это даст возможность обоям хорошо пристать к стенам.

Деление в столбик

Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.

О чем эта статья:

3 класс, 4 класс

Деление с остатком

Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:

Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).

Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).

КАК КЛЕИТЬ ОБОИ научу за 7 минут

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.

Деление трехзначного числа на однозначное

Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:

• 322 — делимое или то, что необходимо поделить;
• 7 — делитель или то, на что нужно поделить:
• частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.

Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.

Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.

Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Деление трехзначного числа на двузначное с примерами

Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.

Пример №1.

Разделим трехзначное число 324 на двузначное 81.

Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.

Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!

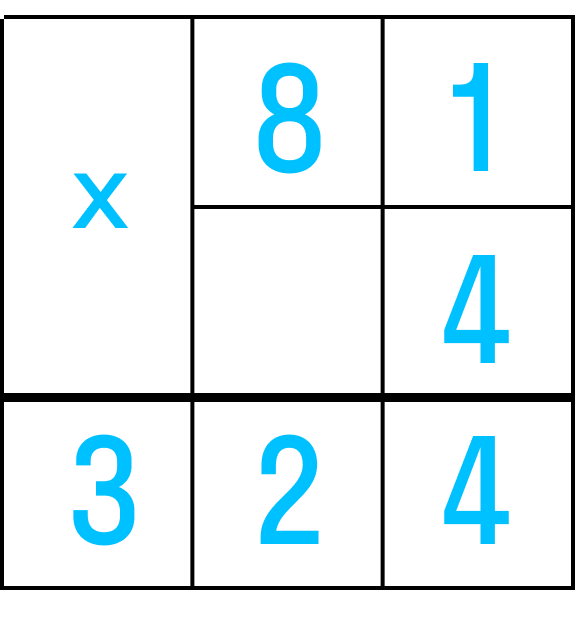
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.

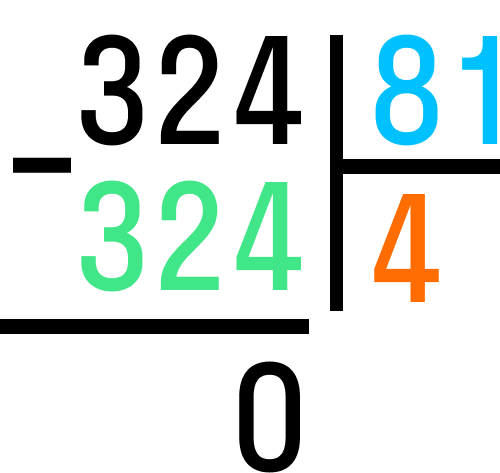
Пример №2.

Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.

Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.

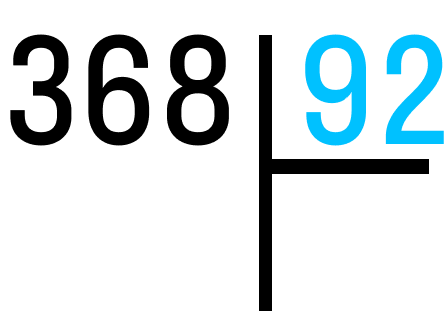
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36_9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.

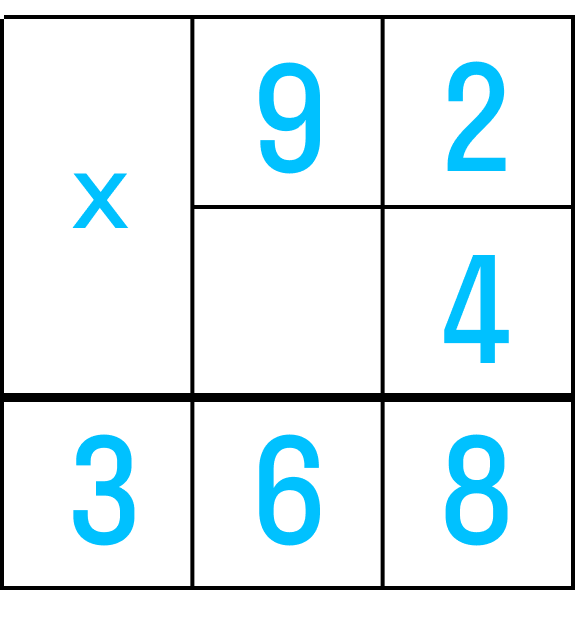
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.

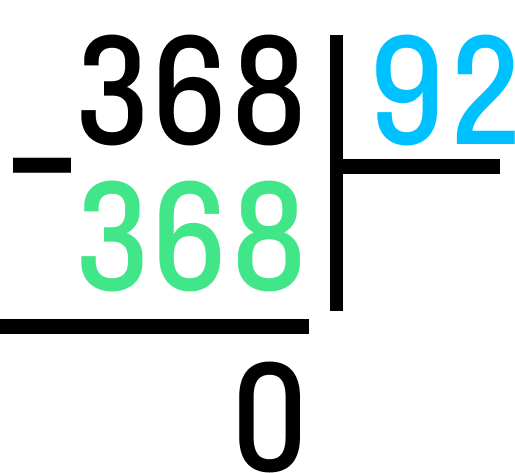
Как делить однозначные и многозначные числа в столбик с остатком

Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.

Пример №1

Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.

Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.

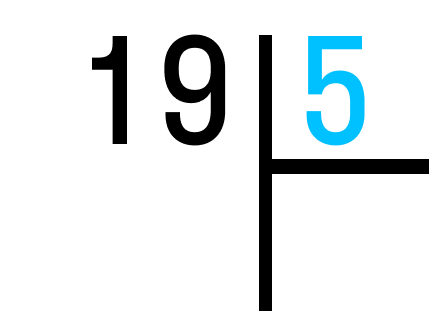
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.

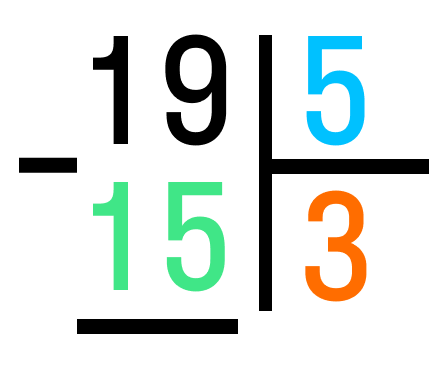
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.

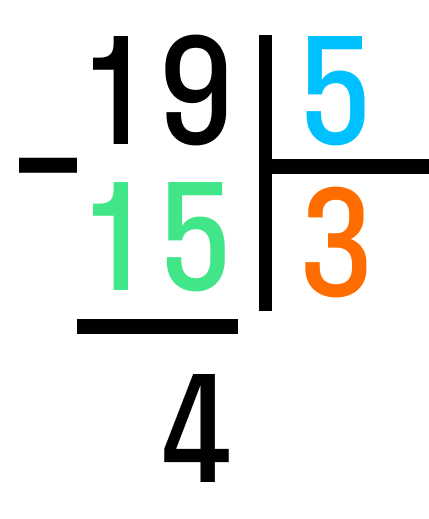
Пример №2.

Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.

Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.

Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.

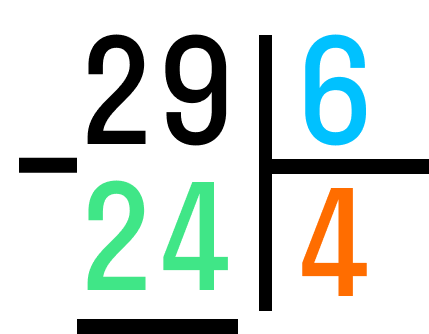
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.

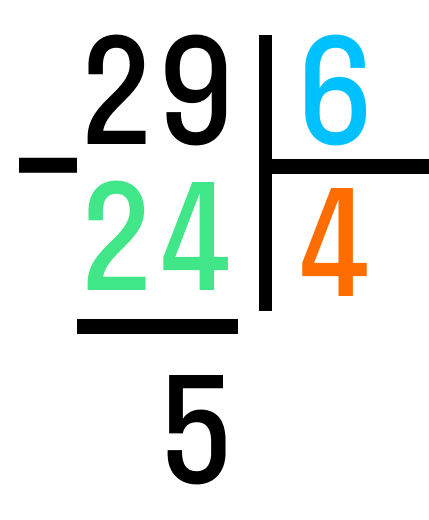
Примеры на деление в столбик для 3 класса

Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.